An important part of Computer Science is related to algorithms: their creation, implementation and optimization. These can range from a purely human process such as making a purchase, to a mathematical process for automated disease detection or diagnosis.
Whatever the origin, all of them include the obtaining of data, the processing of them, and the generation of results as a consequence of the process. This is called an algorithm.
In the mining industry, spatial predictive models and their associated algorithms are an integral part of the development of mining projects and production cycle, through the characterization of geological resources, geometallurgical variables and quantification of associated uncertainty for use in mine planning and economic valuation.
At GeoInnova we believe that the future of spatial characterization of geo-mining-metallurgical variables will be online processing with the addition of new information of different nature and temporality, such as chemical analysis in DH and BH, metallurgical tests, images, spectra, mapping, to then generate spatial models and decision-making processes.
In this context, the optimization and development of algorithms that enable progress in this direction becomes key, so we are working on it focusing on delivering to our customers more accurate and flexible results with reduced execution times.
Parallel Computing: A Brief Introduction
While the heart of algorithm optimization is to use data structures, searching, ordering or calculation methods that are optimal for the problem to be addressed, the possibility of parallel computing reduces execution times significantly and even more so if an algorithm is optimal.
Parallel computing is the technique that allows multiple processes of a single program to run simultaneously by taking advantage of the availability of execution threads that the processors (CPUs) have. This capacity of the central processing units was increased when multi-core processors began to be manufactured and commercialized, allowing even more processing threads to be available than single-core processors.
Later on, multi-core graphics processing units (GPUs) began to be manufactured with the ability to process not only video and images, but also large volumes of data even exceeding central processing units (CPUs).
At GeoInnova, we are aware of the capabilities of GPUs, the potential they have to perform calculations, and how well they can be adjusted to geostatistical algorithms.
Parallel Computing: The first steps in GVN
For GeoInnova the parallelism is nothing new. Since 2015 we have made efforts to find the best technological tools available to implement parallelized algorithms.
As a first step, the NVIDIA CUDA framework was selected for its potential in recent years and, as a test algorithm, the experimental calculation of the variogram, which despite its simplicity is computationally intensive due to the amount of data and variables. The last-mentioned can be prohibitive in blasthole data scenarios, imaging, hyperspectral imaging, and spectra.
The first lessons learned from parallelizing the implementation of the variogram on CUDA-enabled GPUs revealed that while parallelism is a great tool for reducing execution times, the CUDA framework is not flexible enough to address all the issues that would arise in more complex calculations, as well as the difficulty of generating a code, besides the fact that this framework is unique to NVIDIA [Pola et al., 2017].
This first approach resulted in the adoption of the OpenCL framework to implement parallelized algorithms, since unlike CUDA, it can be implemented on any data processing device, whether CPU or GPU, and from all major manufacturers of these devices: Intel, AMD and NVIDIA.
Parallel Computing: The Challenge of Spatial Prediction
The challenge after the previous learning was to generate implementations of the Kriging and Co-Kriging spatial prediction algorithms, which require a lot of computing power and that we set out to optimize and implement using parallel computing on GPUs using C++ y OpenCL.
To prevent from building a laboratory implementation, part of the challenge was to generate implementations that could be used under current mining industry practices such as flexible kriging plans in terms of data restriction, extreme values and use of orientation, variable anisotropy in data search and variogram.
Kriging and Co-Kriging: CoEstim
The first step in implementing these algorithms on GPUs is to optimize them as possible before reaching that point. We obtained the base algorithm from KT3D and COKB3D GSLIB [Deutsch et al., 1992], adapting it for the multivariate case (>10) and managing heterotropic data. The adaptation/translation was done from Fortran to C++. Then, we optimized each of its parts until we achieved a point where we could not obtain the same results with a shorter execution time.
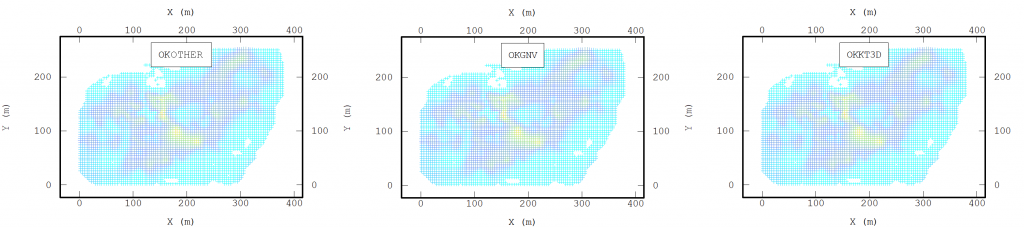
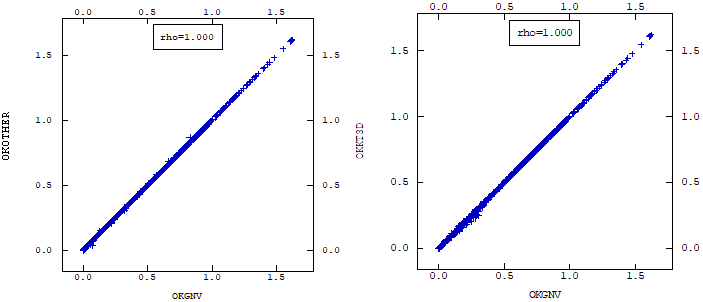
When parallelizing the algorithm, we revisited the algorithm to define which parts of the algorithm would be parallelized and applied two criteria: the slowest process and the independence between calculations. This last criteria is due to the fact that, to avoid bottlenecks in the parallelism, all the execution threads must be independent of each other in order to take full advantage of the processing capacity. Thus, we conclude that the processes to be parallelized would be: the search for neighbors, the calculation of the covariance matrix and its reduction for each point to be estimated.
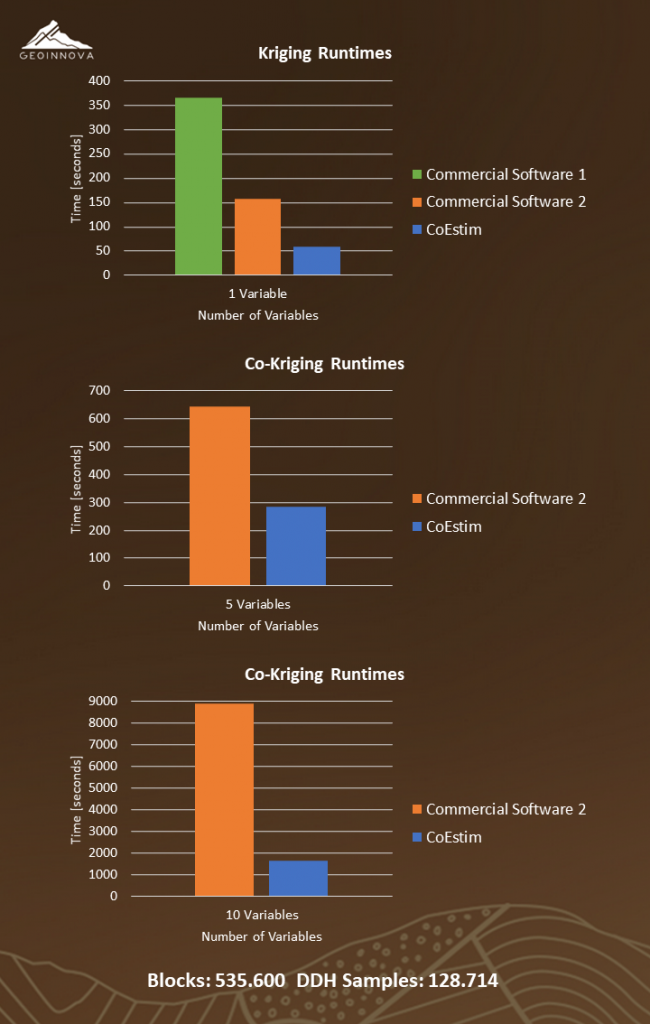
When the processes to be executed and their design were defined, the necessary subprograms to be used on the GPU were then implemented. Once we obtained stable versions, we proceeded to compare execution times, and the results were amazing. The following are the runtimes for CoEstim and two other commercial software applications.
Simulation of continuous variables: CoSim
The second challenge corresponds to spatial stochastic models of continuous variables such as copper grades, contaminants and geo-metallurgical variables. The algorithms associated with these are more demanding in computation and in managing large amounts of information than the algorithms presented above.
The first step was the evaluation of model and algorithm framework selection. We selected the multi-Gaussian framework for its industry penetration and suitability to the vast majority of the deposits and variables we face on a daily basis.
As a simulation algorithm we evaluated the SGSIM algorithm of Gaussian sequential simulation available as source code in the GSLIB [Deutsch et al., 1992] in Fortran as a first option, but we ended up choosing the simulation algorithm TBCOSIM available in Matlab in the 2008 publication of Professor Xavier Emery of the University of Chile [Emery et al., 2008].
The reason for the selection of the rotating bands algorithm is the flexibility that it presents in the multivariable case and the potential for parallelization when using the rotating bands method to generate the non-conditional simulated values and co-kriging for conditioning by the residual substitution method, allowing us to reuse the previously developed CoEstim implementation.
After optimizing the algorithm and generating the parallelized version on GPUs, we named it CoSim.
Although the results were interested in small-medium scale cases, with a large volume of nodes to simulate the memory capacity of the GPUs in the local machines were not enough. Due to the volume of memory required and the volume of information generated, we were forced to move to a distributed computing solution, initially on a local computer cluster and then with cloud distribution.
It is not enough!!: Distributed Systems
After obtaining a parallel base program on GPUs we became even more ambitious and wanted to go further.
What other ways can we further reduce the execution time?
In the computer world the saying “divide and conquer” is frequently used, especially when solving problems. This refers to the fact that a complex process can be divided into less complex and more approachable sub-processes than the original process, and that the addition of these parts provides the expected result. It also applies when multiple machines perform the same process and a problem is divided in equal parts, one for each machine, reaching a result in a lower cost of time.
In the Distributed Systems this premise is applied for different purposes: to divide a process in different machines, each one of them specialized in its task; to generate data backup systems with high redundancy; to generate shared file systems editable by multiple users; to accelerate a process, among others. For our problem we implemented a distributed system to lower the execution time of very expensive tasks, one of them is the Simulation of continuous variables.
After we generated the cluster, we inserted CoSim into it, and programmed the server to perform the division of work. The machines utilized were computers that were available at GeoInnova’s offices. The initial result was a little discouraging: While it allowed us to manage a large volume of data, the machines were very disparate in power, some taking too long and others too little. The launch process was complex and the execution time did not come down to the level we expected.
How do you generate a number of machines with the exact same qualities? Answer: Virtual Machines. But where do we get so much power and quantity? Answer: Google Cloud Compute Engine.
Cloud Distribution
In order to solve the problem of homogenizing the machines where CoSim is running, we used the Google Cloud Compute Engine platform. This platform allows us to generate virtual machines from which we can choose their features from many of the options offered, in addition to having GPUs available for them.
We moved our cluster to Compute Engine, where we use eight virtual machines as runners and one as a server. This way we got the results we expected, and more. The execution times below:
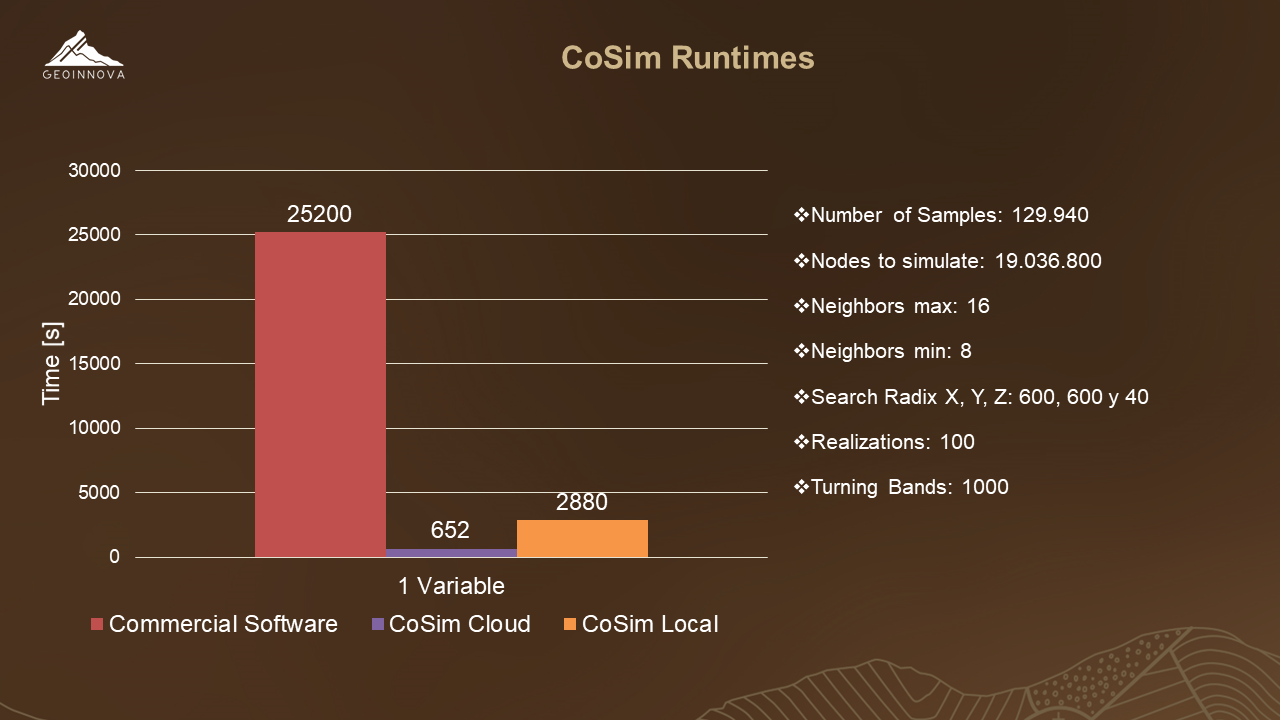
When comparing the Cosim-Local vs Cosim-Cloud implementation we got up to 10 times shorter runtimes in the Cloud version, this is due to the homogenization of the machines and the fact they had a high power GPU. When compared to commercial software the time drop is much more noticeable for both versions of CoSim.
As previously presented, the parallelization of processes represents a significant improvement in execution time, in some cases being up to 10 times faster than commercial software. Naturally, the versions of commercial software that do not have the same implementation on GPUs as the parallelized cases have a longer time and the comparison is not of algorithm but of implementation.
Process distribution also allows an improvement in runtime, especially when you have machines with similar characteristics and high computing power, which is what we achieved in the Cloud version of CoSim. Again, the times of the commercial software versions, not having the same parallelized and distributed implementation, are ostensibly greater, and now the comparison is not only of implementation, but also of hardware.
Real applications
One of the advantages of having the consulting team as a counterpart to the R&D team is the possibility of continuous testing of CoEstim and CoSim in the context of project execution in parallel with the traditional methodologies available in the commercial software. This has contributed to debugging, verifying and improving both applications over the past two years, allowing us, for example, to co-simulate 3 variables on 21 million nodes with 100 realizations in just 1 hour.
Learning and Opportunities
Parallel computing on GPUs or distributed over several machines allows to reduce the computation times of the algorithms associated with the current problems of geo-mining-metallurgical modeling, but more importantly it opens new possibilities of modeling with implications in the management of the mining business, for example, potentially changing the modeling-planning cycles in stages, to a continuum.
Acknowledgements
We would like to thank the SR-181 Innovation and Development Center of GeoInnova, accredited by Corfo, and the consulting team involved in the development of CoEstim, CoSim and distributed computing, as well as the Corfo projects 17ITE1-83672, 16GPI-60687, 15ITE1-48211.
Current R&D Team:
Alan Toledo  , Alejandro Cáceres
, Alejandro Cáceres  , Manuel Hoffhein
, Manuel Hoffhein  , Javier Ortiz
, Javier Ortiz  , Cristóbal Barrientos
, Cristóbal Barrientos  .
.
Historical R&D participants:
Daniel Pola  , David Valenzuela
, David Valenzuela  , Sebastián Blasco
, Sebastián Blasco  .
.
Testers Consulting Team:
Danilo Castillo  , Rodrigo Gutiérrez
, Rodrigo Gutiérrez  , Lucas Contreras
, Lucas Contreras  .
.
References
(1992) Deutsch, C., Journel, A. GSLIB: Geostatistical Software Library and User’s Guide
(2008) Emery, X. “A turning bands program for conditional co-simulation of cross-correlated Gaussian random fields.” COMPUTERS & GEOSCIENCES.
(2017) Cáceres, A., Valenzuela, D. and Pola, D. “GPGPU-based parallel variogram calculation and automatic model fitting.” GEOMIN MINEPLANNING.